Trammels

Take a look at these beautiful designs!

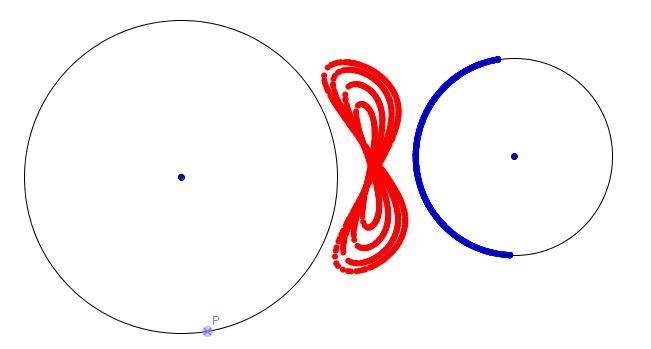
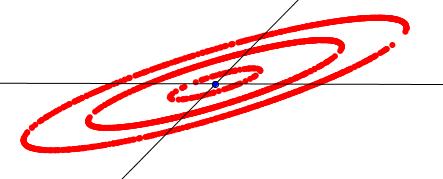
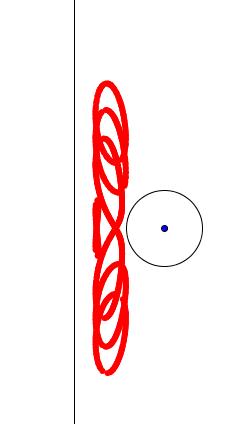
Originally, a trammel refers to an instrument invented by Archimedes as an easy way of drawing an ellipse. The trammel is a rod with a hole at a point; the rod is placed so that its two ends always lie on the x and y axes and the locus of the hole traces an ellipse.

We can generalise a trammel to mean the following: We select two curves, say C1 and C2. We choose a line segment of length l and a point P on the line segment. The line segment is moved in such a way that one end is always on C1 and the other end on C2. As the line segment is moved, the point P traces a curve.

The three figures above show this process. In Fig 1, C1 and C2 are both circles; in Fig 2, C1 and C2 are straight lines intersecting at a point ad in Fig 3, C1 is a straight line and C2 is a circle. The locus of P is shown in red. Different curves are defined by changing l, the length of the line segment.

Some of the questions that can be asked are:

• What is the relationship between C1, C2, l, P and the curve generated?
• Is there a way of selecting these parameters to generate a given curve?
• It is very easy to make a trammel out of a piece of cardboard. Can one develop a gallery of examples?
• It is very easy to draw the curves using Geogebra. Again, can a gallery of examples be made?

There are some files you can download for free here, which will help you experiment more with such curves!